Learning Objectives
- Define population, population size, population density, geographic range, exponential growth, logistic growth, and carrying capacity
- Compare and distinguish between exponential and logistic population growth equations, and interpret the resulting growth curves
- Explain using words, graphs, or equations what happens to a rate of overall population change and maximum population size when carrying capacity changes
- Analyze graphs of population density versus a survival or reproductive trait to determine whether the population is being regulated by density
Population ecology
A population is a group of interacting organisms of the same species and includes individuals of all ages or stages: pre-reproductive juveniles and reproductive adults. Most populations have a mix of young and old individuals. Quantifying the numbers of individuals of each age or stage gives the demographic structure of the population. In addition to demographic structure, populations vary in total number of individuals, called population size and represented by the variable N, and how densely packed together those individuals are, called population density. A population’s geographic range (see figure) has limits, or bounds, established by the physical limits that the species can tolerate, such as temperature or aridity, and by the encroachment of other species. Population ecologists often first consider the dynamics of population size change over time, of whether the population is growing in size, shrinking, or remaining static over time.

Exponential (or Geometric) Population Growth
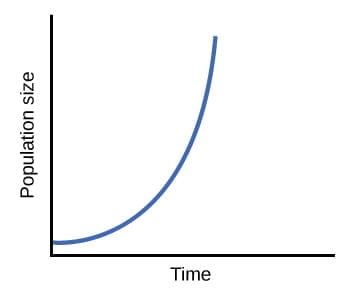
The most basic approach to population growth is to begin with the assumption that every individual produces two offspring in its lifetime, then dies, which would double the population size each generation. Population doubling at each generation is how an ideal bacterium in unlimited resources would reproduce. Graphically, exponential growth looks like this J-shaped curve
Because the births and deaths at each time point do not change over time, the growth rate of the population in this image is constant. Mathematically, the growth rate is the intrinsic rate of natural increase, a constant called r, for this population of size N. r is the birth rate b minus the death rate d of the population. The exponential growth equation

helps us understand the growth pattern over time t: the population size times the growth rate gives the change in population size with time.
Although the value r is fixed with time, the population doesn’t grow linearly in this model because every individual that was born in that generation reproduces. As a result, the population explodes in size very quickly. In nature, a population growing at this dramatic rate would quickly consume all available habitat and resources. In contrast to the model predicted by the exponential growth equation, natural populations have size limits created by the environment.
Logistic Population Growth levels off at a carrying capacity
To consider how resource limitation affects population growth, we need to incorporate the concept of carrying capacity, the maximum population size that the environment can sustain. Any individuals born into this population would increase the population size unless the number of deaths balanced or outnumbered births. If the population size remains the same from one generation to the next, then individuals must also be dying at a similar rate. With exponential population growth, the population growth rate r was constant, but with the addition of a carrying capacity imposed by the environment, population growth rate slows as the population size increases, and growth stops when the population reaches carrying capacity.
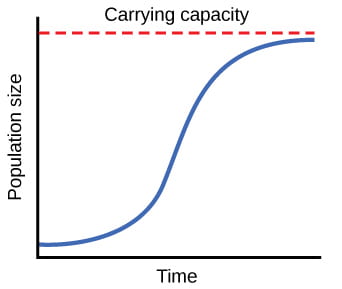
Mathematically, we can achieve this by incorporating a density-dependent term into the population growth equation, where K represents carrying capacity:

Now, the equation shows population growth rate r modified by the density-dependent term, (K–N)/K.
What happens to population growth when N is small relative to K? When N is near K? And when is the population adding the most individuals in each generation?
Population size is regulated by factors that are dependent or independent of population density
Biological and non-biological factors can influence population size. Biological factors include interspecific interactions like predation, competition, parasitism, and mutualism, as well as disease. Non-biological factors are environmental variables like temperature, precipitation, disturbance, pollution, salinity, and pH. All of these factors can change population size, but only the biological factors (except mutualism) can “regulate” a population, meaning they push the population to an equilibrium density, or carrying capacity. Of the biological factors, mutualism does not regulate population size because mutualisms promote population increase through beneficial interactions with another species.
The biological factors of competition, predation, etc. that regulate population growth affect dense versus sparse populations differently. For instance, communicable disease doesn’t spread quickly in a sparsely packed population, but in a dense population, like humans living in a college residence hall, disease can spread quickly through contact between individuals. Density plays a key role in population regulation in the following ways:
- Territoriality: Maintaining a territory will enable an individual to capture enough food to reproduce, where space is a limiting resource.
- Disease: Transmission rate often depends on population density
- Predation: Predators may concentrate on the most abundant prey
- Toxic Wastes: Metabolic by-products accumulate as populations grow
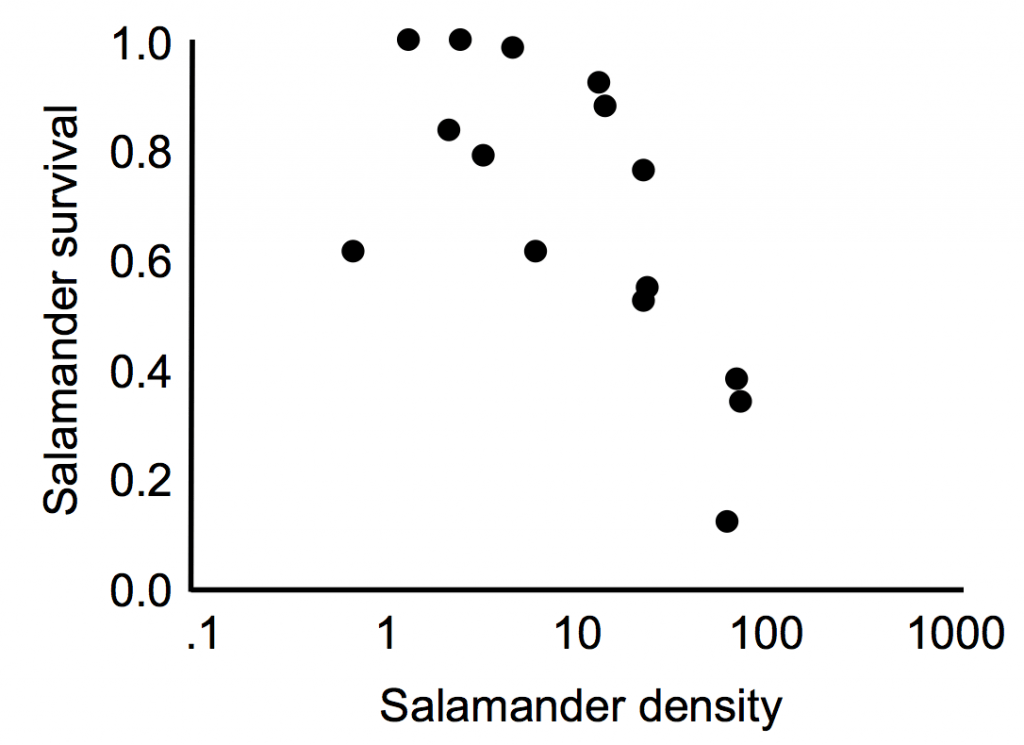
Identifying evidence of density regulation requires a field or lab experiment that manipulates density and quantifies the response in population growth. Often an (easier to measure) proxy of population growth, like survival or reproductive output, stands in as a quick metric of the births and deaths that will impact population growth. The characteristic negative correlation in the image below is evidence of density-dependent population regulation: higher densities yield lower survival.
Here’s Hank Green’s take on Population Growth to help you review these ideas:
UN Sustainable Development Goal

SDG 12: Responsible Consumption and Production – Understanding population size, density, and carrying capacity is essential for sustainable resource management and consumption. By studying population growth, we can better predict how much of a resource can be sustainably harvested or used, which helps create scientifically-informed, sustainable management practices.